Why Topology Matters in Psychoanalysis – Part II

Let’s start with an obvious question that followed from the first article in this series: how is the use of topology in psychoanalysis not just metaphorical? How is it not, even, mystification?

Remember that Lacan is making a bold assertion, as stated in L’Étourdit from 1972:

“Topology is not ‘designed to guide us’ in structure. It is this structure.”

This is a position he maintains right until the end of his life, including at his last ever public speaking appearance in Caracas for Seminar XXVII.

This second article will answer this question with examples of how we can think about the problems in a person’s life – the problems that psychoanalysis is concerned with – as having topological properties.

Topology is about a delimitation of space. This could be signifying space, physical space, relational space – its topological properties persist regardless of the nature of the components of that space, or the deformations that space undergoes, as we saw in part one.

Delimitation means separation. The German term for separation is trennung, and topologists talk about Trennungsaxiom, or separation axiom, to describe the ways that topological space can be delimited, with varying degrees of strength. We will come back to this idea later on.

For now, we can say that the delimitation of space, and the strength with which its separation is inscribed, is a crucial problem in understanding all kinds of phenomena of interest to psychoanalysis. Let’s start with a few simple examples from the ‘clinic of the everyday’:

Phobia – very often involves a delimitation of space. We can think of the way that an agoraphobia, or a relatively common phobia about crossing bridges, marks out the thresholds of a space. To take an old Freudian example, in the case of Little Hans, we can think about the way in which the horse phobia dictates when he can and can’t go outdoors (SE X, 22-24).

Obsession – the problem of passing from one space to another haunts obsessional rituals and acts with an uncanny recurrence. They are very often concentrated at the point where one space transitions to another. Opening and closing doors, turning on and off lights, or catching trains or planes from points A to B are common focal points for obsession. Similarly, we can think of the artificial delimitation of space in cases where someone feels unable to step on the cracks between paving stones, for example. So why this recurrence?

Pornography – why do so many porn movies involve opening the door to someone? We find this in both typically male and female scenarios, both romantic novels and hardcore porn. We may not view it as pathological like obsession or phobia, but it is interesting that in pornographic scenarios some kind of scene is staged involving a crossing of a threshold.

.
We are not yet making any claims about topology, but simply stating some problems it might help us to explain, problems which are about this same trennung or separation.

And what kind of space are we really talking about here? Physical or metric space doesn’t seem quite to cut it. Although components of physical space like a door or a bridge may appear in phobia, obsession and porn, it would be facile to believe that the real problem in phobia is the bridge that can’t be crossed; or that in obsession a ritual about doors is really only about doors. This is why therapeutic approaches like CBT, which target only the site of the complaint, eventually lead to symptom substitution.

As we saw in the first article, if we think only in terms of physical space we can’t solve a problem like the seven bridges of Königsberg. We are instead talking about a space that can be conceived regardless of the elements that compose it. This is the justification for looking to topological space to address phenomena as disparate as the three above, but which are all of psychoanalytic interest.

How This Works in Practice
Example 1 – The Rat Man

Let’s take one of the most famous cases from the history of psychoanalysis, one we have looked at in depth before: that of the Rat Man.

In their paper ‘Psycho-topologies: closing the circuit between psychic and material space’, Virginia Blum and Anna Secor point out that the little maps the Rat Man draws Freud to illustrate his mission to repay the money for his glasses – the feature of the case which Lacan focuses on – bears a topological resemblance to the bridges of Königsberg problem we discussed last time.

“… The patient develops a tortuous scheme necessitating a train trip that could not possibly occur in real time and space, whereby he attempts simultaneously to repay and avoid repaying the crucial debt…. His compulsive journey shows him seeking to solve or to overcome a psycho-spatial problem….The coordinates of his map/graph – his nodes and lines, vertices and edges – are, like the bridges of Königsberg, capable of endless distortion without any shift in their basic relations.” (Blum and Secor, ‘Psycho-topologies: closing the circuit between psychic and material space’, p.17).

When he looks at the Rat Man case history in ‘The Neurotic’s Individual Myth’ in 1954 we see Lacan trying to find a new model to conceptualise the entanglement of relations in the life of Freud’s patient. With structural anthropology – and in particular with Levi-Strauss’s conception of myth – he thinks he has found it.

Summarising his idea in a 1957 interview with L’Express, Lacan says of the Rat Man:

“He is descended from a legendary past. This prehistory reappears via the symptoms that represent that pre-history in an unrecognizable form, that weave it into myth, represented by the subject without awareness. Since it is transposed like a language or a writing, maybe transposed into another language, with other signs; it is rewritten without the modification of the liaisons; like a figure in geometry is transformed from a sphere to a plane.” (reproduced here, my italics).

Note this last point. Just like thinking of the physical links of the bridges of Königsberg as instead being nodes and vertices, so we can do the same with the relationships in a person’s life. Instead of describing bridges we are describing inter-human relations of love, hate, and debt. The relations may be deformed by (chronological) time or (physical) space, and one person may be replaced by another, but the liaisons themselves – the relationships – remain the same. As Lacan writes,

“Everything happens as if the impasses inherent in the original situation moved to another point in the mythic network, as if what was not resolved here always turned up over there” (‘The Neurotic’s Individual Myth’).

Lacan has an intuition that there is a network of relations which have very peculiar characteristics. Looking just at the Rat Man’s personal biography – his love for his ‘Lady’, the ambivalence towards his father, the hatred of the ‘Cruel Captain’ – isn’t enough to explain it.

What we see in the maps above that the Rat Man drew for Freud is like a nucleus of the neurosis. Just as the elements of the map and the story that goes with it are jumbled and nonsensical in spatial or chronological terms, so the relations in his life make no sense when looked at in terms of a continuity of emotion (the affective ambivalence which has been the focus of almost all commentaries on the case), or even the continuity of time (not only the father’s debt being trans-generational, but the fact that Freud even tells us how the Rat Man forgot his father had died (SE X, 174). What we see in the map looks more like a condensation: time and locality don’t matter; the map tells us more about the nature of his relationships insofar as it indicates these elements can be reconfigured, in the same way a topological space like a torus can be reconfigured.

Over the next 20 years this intuition led Lacan to explore topological models that exhibited these same properties – the torus, the Mobius band, and the Klein bottle were all, as we saw in the first article, examples of these.

But pursuing these ideas right up to his death in 1981 Lacan became obsessed with one particular topological model: the Borromean knot. After his death, what might call the ‘clinic of the Borromean knot’ was interpreted by many of his followers as representing his legacy. It was deemed to be the new frontier, the cutting edge, of Lacanian clinical treatment.

We will go on later to look at the history of this project since Lacan’s death; how the generations of Lacanian psychoanalysts after him have taken it forward; and some of the radical implications it suggests.

Example 2 – ‘A Calculus of Convergence’

There are some Lacanian analysts who think about the problems they face in the clinic topologically. Here is one such example.

In her paper ‘A Calculus of Convergence’, Nathalie Charraud presents a case which turns on an intervention she makes with one of her patients. This constitutes what she calls a “point of convergence” (Drawing the Soul, p.219). The analysand tells her three things:

Firstly, that she needs to end the analysis because the man who is paying for it is living with another woman, making her effectively his mistress.

Second, she has a nightmare where she is walking down a long corridor which opens out into a desert. She is stiflingly hot, and wakes up with a strong urge to vomit.

Third, she needs a work permit to stay in France but, terrified of applying for it herself and being rejected in person by the prefecture, she hires a lawyer to apply in her place.

.
Charraud responds with the following: “there’s rejection”.

This intervention has a profound effect on the direction of the analysis – it is the catalyst for an improvement in the analysand’s well-being. How?

Charraud shows how the details the woman tells her can be put into a signifying constellation conceived of as a topological space. Let’s look at its elements.

The French rejeter in “there’s rejection” has all kinds of connotations that are pertinent to how the analysand describes her dream and the circumstances of her life at the time. These include ‘to reject’, ‘to expel’, ‘to dismiss’, ‘to throw up’, and Charraud’s intervention plays on the ambiguity generated by these connotations. Charraud explains it like this:

“The signifier ‘rejection’, in the case of my analysand, is clearly a master signifier, which represents her in the vicinity of a certain number of other signifiers S2 (her family, the Prefecture, various consulates and embassies” (ibid, p.220, my italics).

In simple terms, we can represent these relations like this:

To see how we get from this to a topological conception we will lean on the work of those analysts most deeply immersed in this theory. Eric Laurent’s ‘Lecture Critique II’ in L’Autisme at la Psychanalyse and Bernard Burgoyne’s collection Drawing the Soul – from which Charraud’s case is drawn – are key texts here.

The branch of topology that Lacan was interested in – and from which all other branches of topology stem – is known as ‘point-set’ (or ‘general’) topology. A set is a collection of objects, and the elements within it are points. A set of points, and the interrelations between them, may constitute a topological space. And with her intervention, Charraud will establish a topology through the interrelation of the three associative elements provided by her analysand.

Here are some examples of topologies that can be generated from three-element sets, like the one in Charraud’s case:

Image credit: https://www.gipom.com/search/Point-set+topology/images?lang=en

Let’s take each point in a set as a signifying term. Associated with these signifying-points are what topologists call a neighbourhood. A neighbourhood is essentially a subset – an arbitrary collection of points that give structure to a topological space. We can see some examples in the image above.

Notice that although the topologies – the way these neighbourhoods are constituted – vary, the elements in the structure, the points, do not. As we saw in the first article, this is the fundamental character of a topological space – the ability to retain its properties in spite of deformation. This is how the bridges of Konigsberg problem was solved. This is also a property shared by the Klein bottle, the torus, and the Borromean knot, which was why Lacan was so fascinated by playing about with them in his later life.

As the neighbourhoods of any point have to sit entirely within a set, we can think of the network of all possible neighbourhoods as constituting a language (in the Lacanian sense of a network of signifying elements unhinged from any referent).

Within this language we have other associative elements to the patient’s story which constitute points in their neighbourhoods. Charraud draws these out:

“1. To go, to leave, etc (partir, quitter…)
2. To vomit, disgust, etc (vomir, degout…)
3. Prefecture, papers, passport, etc (prefecture, papiers, passeport).” (ibid, p.224).

The analysis goes on, and these associations are further connected to the theme of paternal rejection (rejet paternel):

“To go, to leave my consulting rooms (partir, sortir de mon bureau);
To be stifled (elle etouffe);
How she chose her profession (comment elle a choisi sa profession).” (ibid, p.224-225).

Charraud labels these a “family of sets” (ibid, p.223), and notes that as they draw closer together there is a kind of condensation – or, to use the term in her title, a “convergence” – of the associative material, “such that successive intersections within the family give something smaller and smaller, something more and more precise” (ibid, p.223). She calls this effect a ‘filter’ but as Burgoyne notes in the footnote to his translation of her paper (ibid, p.226) this “filter” or “family of sets” is equivalent to a neighbourhood. Charraud’s ‘rejection’ is a signifier which hinges these associative elements. It has the effect of marking out these neighbourhoods from the signifying space of the analysand’s life, and thus generates a topological space.

But is this the end of the story? After all, if things were as simple as this a psychoanalysis would be easy. The application of topology to psychoanalysis would amount to forming neighbourhoods between sets of signifying points.

To return to the quote at the top of this article, Lacan says topology doesn’t guide us in the structure – it is the structure. We have talked about the properties of a structure – and specifically, its capability to retain these properties regardless of the deformations that structure might be subject to. But we haven’t yet looked at what Lacan identifies as the “cause”, and all the way throughout his later work Lacan is anxious to find a place for a cause in this structure. This begins with the discussion of Aristotle’s tuchê in Seminar XI from 1964 and runs right through to the work on topology in the 1970s. All the while Lacan is trying to specify something which is inherent to the structure – even at its innermost point – but not part of the structure as such. A remnant, perhaps, of the construction of the structure itself.

Lacan calls this the object a.

In his most famous topological structure – the Borromean knot – he places it at the heart of the structure:

(Seminar XXII, 10th December 1974).

Lacan’s idea – even in the midst of his adventures in topology – is that a psychoanalytic intervention, in order to be effective, has to have an effect on the object a as cause. Otherwise, to paraphrase Freud’s amusing comparison from ‘’Wild’ Analysis’ in 1910, it’s just like handing out menus to cure a famine (SE XII, 225).

Therapeutically, treating a problem like addiction demonstrates this most starkly. Producing a convergence of signifying terms into a neighbourhood may deform or remould the structure, but the structure itself is contingent. As Charraud’s example shows, it can be rebuilt around a new signifier – like “rejection” – but this leaves the cause – object a, at the heart of the structure – untouched.

One way to think about object a is as the nucleus of an unbearable enjoyment experienced as suffering. It is at the root of what is like an overdose of enjoyment, a “backhanded” enjoyment as Lacan calls it in Seminar X (23rd January 1963), which “begins as a tickle and ends in an inferno” (Seminar XVII, 11th Feb 1970).

In Lacanian terms, we call this excess of excitation ‘jouissance’. It is the real enemy of any psychoanalytic intervention. The aim of analysis is to loosen the bond to object a, where proximity to it produces a jouissance that cannot be mastered. The task is then to evacuate this jouissance to discrete margins in the person’s life, or in their body, a process that mimics the ‘symbolic castration’ which Lacan views as the price of becoming a socialised being. If topology is about the delimitation of space – as we began this article by arguing – the practical relevance of being able to do this in order to master jouissance is therefore extremely pertinent.

In the case she presents, Charraud shows how this works. She describes the effect of her interpretation as “a spiral of meaning which itself turns about a hole occupied by the object [a]” (p.221). The object a, Charraud writes, is “a point of convergence, if you regard it as a topology of signifiers.” (ibid, p.223).

Charraud’s idea is that a tightening of neighbourhoods around this object a, neighbourhoods which are hinged by the signifier rejeter – replete with all its connotations in French of throwing up, expelling, or throwing out – isolates it. We see the mark of the object a in the urge to vomit that the patient experiences when waking from the dream, a violent intrusion of something of a different order to, but bound together with, the signifying network. As we often see in psychoanalysis, what cannot be represented in one register (here, the symbolic) reappears in another (the real of bodily suffering).

The effect of the analysis is to loosen this tightening of the signifier to the object a. Charraud explains this in the following terms:

“What is interesting is the difference between the initial situation and that at the end. The initial structure displays a convergence towards one signifier, that is, a signifying stasis – or, again, a symptom, in the sense of a condensation – where the signifier ‘rejection’ finds itself stuck to the object. It seems that the effect of the interpretation would have been, on one hand, the unsticking of the signifier in relation to the object – which can be seen in the fact that her problems with her papers will sort themselves out, and that she will not obey her compulsions to leave. On the other hand, there’s an effect of subjectivity in so far as she remembers something primordial in her existence – the choice of her profession: primordial in the sense that she had left everything behind, and crossed the ocean in order to bring it into being. A short time after this session, she found herself in the position of being able to pay for her sessions herself” (p.225).

The effect of this unsticking is a dispersal of jouissance away from the object, a kind of draining or evacuation of malevolent excitation through an intervention which links a number of signifying sets into a neighbourhood. Charraud’s case shows that the application of topology to psychoanalysis is not simply a matter of describing the relations between signifying elements in a person’s life. It is more fundamentally to have an effect on the jouissance that animates their life. The real enemy of a psychoanalytic process – the thing that keeps a symptom in place, is the malevolent enjoyment attached to it: jouissance.

Example 3 – Autism and the work of Le Courtil

Today, the problem to which topological theory is most readily applied in Lacanian practice is in the clinic of autism. Le Courtil in Belgium is the most famous clinic in this respect, having been featured in Mariana Otero’s beautifully light-touch 2014 documentary, Like an Open Sky (À ciel ouvert). But there are also similar insitutitions such as Antenne 110 and Le Centre Thérapeutique et de Recherche de Nonette, as well as a network of other institutions which work with autistic youngstes from a similar perspective, known as the R13 (for a full list see here).

Topologically, what practitioners in the Lacanian orientation are trying to do in the treatment of autism is to introduce a delimitation of space. This can be done even in the most modest, minimal way. In Like an Open Sky we see the way that the clinicians of Le Courtil go about this with the autistic children and adolescents they host. As one of the supervisors summarises the approach in the film, “We have to handle things via a break, writing or counting, and that’s what the art of the work will be”.

Why is this delimitation of space necessary? The Lacanian theory is that autistic subjects face being overwhelmed by a jouissance against which they especially are defenceless. This jouissance could be experienced as coming from the Other (for example, the institution) or from the body itself, but it is always ‘Other’ in the sense of being felt as invasive or excessive.

Le Courtil helps its young intake construct their own techniques to deal with this through various ways of creating a delimitation of space. In Like An Open Sky – and the published interviews with analysts of the centre which accompany the documentary – we see many examples of the solutions they find:

Writing – Speaking about one of the children at Le Courtil, Bernard Seynhaeve tells how, “Writing, even if it’s gobbledygook, in its very materiality, in its applied gesture, allows him to construct a rim, to give an edge to jouissance.” (p.66). For this child, “By writing, there is something of jouissance that finds an edge.” (p.84).

Gardening – Similarly, Véronique Mariage talks about using gardening with the children as a way of helping them to establish the boundaries of a space: “There aren’t just the plantations. For Jerome, for instance, what was important was to have a patch of ground bordered by a kind of wide ditch, as though his garden were a castle. He is always constructing castles, in card, and so on. For the autistic child, this is his protection.” (p.68).

Jigsaw puzzles – Alysson, a third child in the documentary, finds solace in jigsaw puzzles. “Since she was four years old, puzzles have been the most constant object that calms her”, the analyst says. Alysson is both horrified and fascinated by her own body, and we see her battling constant anxiety about what is going on inside her body or underneath her skin. Through working on jigsaw puzzles she finds an antidote to this anxiety. Jigsaw puzzles perform the role of a supplement for a body that doesn’t hold together. In Lacanian terms, this lack of corporeal integrity denotes a disturbance in the imaginary register, and as we saw above a problem or impasse in one register reappears in another. As Alexandre Stevens, Director of Le Courtil comments, “… I think we perceive how this young girl, deep down, is in pieces. As for a diagnosis, I immediately think of schizophrenia, with this intense corporeal break-up, this concern, this dismemberment even, as she sees her body in pieces.” Solving jigsaw puzzles, for Alysson, provide a highly idiosyncratic but effective solution insofar as they offer a way of framing a series of fractured images into a unit.

Open sets and the Freudian defence mechanisms

Psychoanalyst Bernard Burgoyne has written and lectured extensively about autism and topology. In his paper ‘Autism and Topology’ he puts forward the idea that the autistic child’s inability to defend against a jouissance from the outside results from a difficulty in dealing with different kinds of spatial realities. These spatial realities can be thought about in topological terms.

Let’s explain how this works with some topological theory.

In any set, a signifying point will have associated with it a collection of other signifiers or phrases, which taken together can form a neighbourhood within the set. As we saw earlier, each point can be thought of as a signifying term and their neighbourhoods a language.

In topological terms, to define a set out of a space you have to identify its frontiers. These are known as limit points, so a limit point of a set is a point that is used to define the boundaries of a set.

A closed set is a set which contains all its limit points.
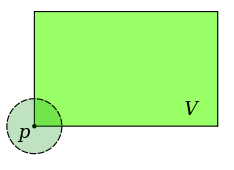
By contrast, an open set doesn’t contain any of its limit points:

So for a set to be open all of its points must have some space around them which remains entirely within the set. This is also the special characteristic of neighbourhoods:

For example, this is a neighbourhood:

But this is not:

As Burgoyne writes,

“A neighbourhood of a point has the property that there always exists within it an open set surrounding that point. That is, a neighbourhood of a point always gives the ability to retreat to a collection within it that protects from intrusion from outside. In a space of phrases, a neighbourhood of a particular phrase would allow a retreat into a collection of phrases within, any point of which is protected from intrusion by sequences of phrases in the exterior.” (p.202-203).

Burgoyne’s idea is that an open set is the equivalent to the Freudian defence mechanisms. The child’s response to what in Lacanian theory we refer to as symbolic castration is to build out a series of open sets. The signifying possibilities open to the subject are therefore the chain of open sets it has been able to construct. Open sets allow defences against intrusions from points or signifiers from outside the set – in Lacanese, from the demands of, or jouissance of, the Other. So how strong a person’s defence against jouissance is depends on how many open sets are available to them.

Open sets have to be capable of separating any two points from each other. For a distinction between signifiers to exist a separation of points through open sets must occur, such that no open set has the same point in common.

As we saw at the start of this article, spatial realities can be distinguished by the strength of separation between their open sets. Topologists refer to these different separation axiom as T-n levels, from the German term for separation, trennung. In ‘Autism and Topology’, Burgoyne looks at four of these Trennungsaxiom (or separation axioms), going from the weakest form of separation (an indiscrete topology) to the strongest (a discrete topology). In the terminology, this progression is known as the ‘lattice of topologies’.

“T0 has some separation properties, but they are very weak; T1 has somewhat stronger separation properties [referred to by topologists as Hausdorff space]; T2 has build into its structure considerably stronger separations; and M is just a name for the familiar metric spaces… separation properties in M are very strong indeed” (p.208).

Burgoyne believes that we can use these trennungaxiom or separation model as an alternative to the classical developmental models that both psychoanalysis and cognitive-behavioural theories have traditionally relied on. His wager seems to be that the classical psychiatric/psychoanalytic diagnostic model can be mapped onto these trennung levels, from ‘extreme’ autism at the lower levels to ‘normal’ neurosis as metric space. They are about degrees of separation best conceived in terms of in topological space:

“The separation principles at play in T0 and T1 spaces seem to provide the terrain where differentiations between schizophrenia, autism, and paranoia can be established” (p.210).

In short, the problem for the autistic child, as Burgoyne argues, is that the strong degree of separation required to parcel off signifying points as simple as ‘You’ and ‘I’ into distinguishable open sets has not been instituted. The autistic child is stuck in the indiscrete space “between the Hausdorff and T0 regions of the lattice of topologies” (p.210). This is why their relations with others are so problematic, or why they appear to be caught in an impenetrable world completely isolated from the outside. The strength of separation between signifying points in a Hausdorff space allows for a degree of distinguishability or distance they have not been able to accede to.

Semblance, Pretence, Invention

So how does Le Courtil deal with this problem? How does it help its young autistic residents to institute this richer separation in order to get distance from the demands of the Other, or the invasive jouissance they are plagued by?

In Like An Open Sky one of the ways we see this happening is through a pretence or make-believe. By taking on the role of the Other through a semblance, by staging little role plays with the children, a separation can be made from the Other but without the difficulties of having to encounter it head on. “The main thing, for me,” one of the analysts says, “is to see the pretend become possible…. The children can say things in these scenes they can’t say otherwise.” One child is encouraged to play the role of the mother or the teacher, while the analyst plays the role of the child. Importantly, the content of the scene is not prescribed, in contrast to the usual methodology at an institutional level of introducing rules to regulate behaviour towards an educational goal. Rather, the child chooses the theme he or she wants to stage. “In other words”, the analyst explains, “she plays what she has to deal with”.

Le Courtil’s role here is to organise a frame in which this semblance can be staged and then maintained. The frame is not the institution but the scene itself, and it is only if the scene becomes too real that the analyst intervenes to stop it. Otherwise this role playing is enough to establish the distinction between self and Other that autistic children struggle with.

The same semblance technique can be employed where the child has to confront the problem of bodily jouissance. Here is a particularly charming story of a solution one of the children developed for himself when his hand started trembling uncontrollably as he tried to eat breakfast:

Why does this work? If we think of the sum of all signifying possibilities as the number of open sets available to the child, speaking in English offers a shorthand way to expand the series of open sets to develop a richer lattice of topologies. As Burgoyne’s theorises, open sets allow for a protection against intrusion from the outside, and so establish some distance from the jouissance of the Other that invades the body in this child’s case and is felt in the symptom. Burgoyne’s comparison to the Freudian defence mechanisms is apt. It might remind us of Anna O’s solution to rouse herself from the series of hallucinations in which a black snake is coming towards her sick father while she is paralysed at his bedside:

“When the snake vanished, in her terror she tried to pray. But language failed her: she could find no tongue in which to speak, till at last she thought of some children’s verses in English and then found herself able to think and pray in that language.” (SE II, 38-39).

This approach, of allowing the child to invent its own way method of coping through play or pretence, has a significant therapeutic advantage: it requires no allegiance to Lacanian theory or knowledge of topology whatsoever. It can be adopted equally easily by behaviouralists or those with a cognitivist approach because it allows the child to invent a system from its own interests, its own domain of subjectivity. It requires no hypothesis about aetiology, psychodynamics, or outcomes. It simply allows the child to develop its own solution to lead where it will.

Invention, Symptom, Sinthome

The subtitle of the compendium of interviews accompanying Like An Open Sky is ‘Invention from day to day’. Another word to describe an invention is a symptom. In Lacanian terms – particularly in the way Lacan uses this term in his later work – a symptom is not necessarily a malevolent or pathogenic thing. In fact, it can be quite the opposite – a ‘big’ symptom can offer a way to organise the life of the subject.

Invention is a therapeutic application of what Eric Laurent has called the ‘knots programme’. In his later work, Lacan believed that each subject can invent a solution for him- or herself which functions as a supplement to bind together the three registers of the real, imaginary, and symbolic that he had envisaged with the topological model of the Borromean knot. He calls this supplement the sinthome.

Image credit: http://www.lituraterre.org/Illiteracy-psychoanalysis_and_topology-The_Sinthome_by_Lacan.htm

Lacan claims that sinthome is an archaic way of writing ‘symptom’ (Seminar XXIII, 18th November 1975), and it is true that in French symptôme and sinthome are pronounced identically. We can think of Alysson’s jigsaw puzzles as precisely the kind of supplement that Lacan is talking about here: an element that has a special place is a subject’s life by virtue of its function to stabilise the Borromean apparatus of their reality.

The Knots Programme and the Clinic of Supplementation

We can see how Lacan’s introduction of the sinthome in the mid-1970s is a revision of his original idea from the 1950s whereby any subjectivity structure, neurosis or psychosis, goes through what Laurent has called the “logical operator” of the Name-of-the-Father. What changed Lacan’s mind?

Lacan lost faith in the Name-of-the-Father to hold together the symbolic order. Lacanians now recognise this loss of efficacy and debate this, as the title of the 2012 Congress of the World Association of Psychoanalysis attests: ‘The Symbolic Order in the XXIst Century – It’s Not What It Used To Be’. With the theory of the sinthome and the knots programme at the end of his life we have a radically different idea, and if we work through its implications we can see just how radical it is.

If everyone builds their own solution – which might be a phantasy, a ritual act, a delusion – the psychiatric/psychoanalytic categories no longer seem quite so important. Instead, all that matters is the way the knot is formed for each person, in however idiosyncratic a way.

We can detect a tacit acknowledgment of this from the burgeoning of clinical categories in the latest editions of the DSM. Every form of possible solution – every sinthome – is taken as a sign of a disorder, but what isn’t looked at is the function that symptom performs in an individual’s life. This has resulted in a DSM-V so fractured and vast that it has become useless. The fact that the National Institute of Mental Health in the US recently issued a statement asserting the need to move away from the DSM classification model as a result attests to this.

If the question of neurosis or psychosis has always turned on the institution or foreclosure of the Name-of-the-Father, faced with the inefficiency of this quilting point, and the fact that the subject can find another supplement to do its job in the form of a sinthome, do we not have to ask what the difference between neurosis and psychosis is actually founded on any longer? Again, a tacit acknowledgement of this might be found in the revived interest in so-called ‘ordinary’ psychosis in the Lacanian community (and beyond) over recent years.

At the end of his paper ‘The Clinic of the Borromean Knot’ Pierre Skriabine, one of the leading French Lacanians working in the field of topology, hints at something similar – a new clinic of the Borromean knot:

“[Lacan’s topology of knots]… brings neurosis and psychosis closer to each other – at least with respect to the function of supplementation as correlative to the generalisation of foreclosure as structural – while maintaining the radicality of what separates them. It thus announces an entirely new differential clinic, and one which remains to be constructed: a clinic of supplementation indexed on the Borromean knot” (Lacan: Topologically-Speaking, p.267).

This is perhaps what Lacan’s legacy means in psychoanalysis today. At the end of his life, and at the end of his adventures in topology, we are left the “knots programme” as the new therapeutic paradigm.

By Owen Hewitson, LacanOnline.com

 

All content on LacanOnline.com is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.